Речка движется и не движется

«Речка движется и не движется!
Вся из лунного серебра.»
(Позывные радио МАЯК)

В задачах механики твердых тел с сухим трением бывают парадоксальные ситуации, когда задача не имеет решения или имеет неединственное решение. Это так называемые парадоксы Пенлеве, названные в честь французского математика и политика (Пенлеве был премьер-министром Франции в октябре 1917 года, как раз в те дни, когда в Британии приняли Декларацию Бальфура о том, что Палестина принадлежит еврейскому народу, а в России произошел октябрьский социалистический переворот). Дело в том, что направление вектора силы кулонова (сухого) трения зависит от направления скорости движения (точнее, направлена в противоположную сторону). В парадоксальных ситуациях вы делаете предположение о направлении движения, например, тело движется в сторону увеличения координаты Х, а, следовательно, трение направлено в противоположную сторону. Но решение на основе такого предположения получается с движением в сторону уменьшения координаты Х, т.е. сонаправлено силе трения, что невозможно. Тогда вы делаете предположение о направлении движения в сторону уменьшения координаты Х (а трения в противоположную сторону), но в этом случае решение получается с движением в сторону увеличения координаты Х. Выходит, задача не имеет решения.

Paul Painlevé (1863 – 1933)

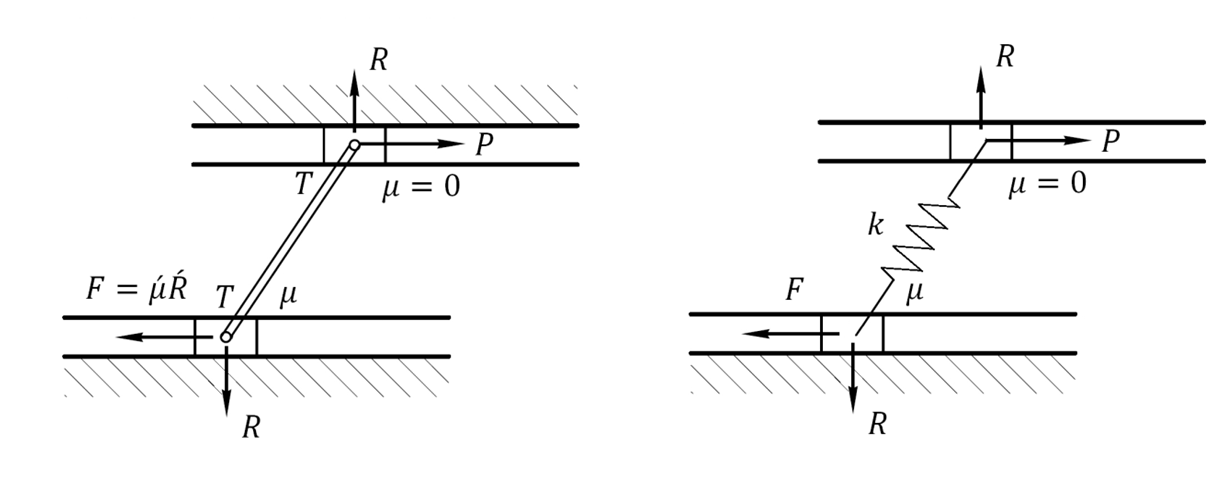
A setup for the Painlevé paradox: two sliders (one frictional and the other is frictionless) connected by a rigid bar; the paradox is resolved if the bar is assumed to be elastically deformable with the stiffness k.

Существует множество подходов к объяснению парадоксов Пенлеве. В частности, считается, что парадоксы вызваны тем, что абсолютно твердых тел не бывает. На практике все тела хоть немного деформируемы. Если предположить деформируемость (то есть добавить в задачу упругость), то парадокс обычно исчезает. Но в этом случае возникает другая проблема: задачи теории упругости с трением могут вести к динамическим неустойчивостям. Если вдуматься, то это понятно. Ситуация, когда скорость, направленная в одну сторону, приводит к движению в противоположном направлении, а движение в противоположном направлении, наоборот, приводит к движению в изначальном направлении, и так далее, очень похожа на неустойчовость, когда система идет в разнос.

Один из подходов к любым логическим парадоксам состоит в модификации системы понятий. Стандартное предположение о движении системы состоит в том, что она либо покоится, либо движется. Можно сказать, что логическая функция принимает два значения Движется(Система)=истино либо Движется(Система)=ложно. В случае парадокса мы имеем ситуацию Движется(Система)=не определено. То есть нам приходится отказаться от системы двоичной логики и от закона исключения третьего.

Движение и покой были противоположными категориями для средневековых схоластов-аристотельянцев. В средние века было сломано много копий при обсуждении вопроса о том, останавливается ли тело при смене направления движения когда достигает крайней точки при колебаниях. Для нас ответ на этот вопрос очевиден: конечно, в какой-то момент мгновенная скорость становится равной нулю, а затем меняет знак. Но чтобы оперировать понятием мгновенной скорости, потребовалось изобрести дифференциальное исчисление, что произошло только в ХVII веке.

Троичная логика, в которой не действует закон исключения третьего, то есть то, что не «истино» и не «ложно» может принимать третье значение, напимер «не определено», на мой взгляд может здесь быть полезна. В этом случае мы имеем три состояния: покой, движение, неопределенность (или неустойчивость).

Могут возразить, что в такой классификации нет необходимости. Можно в рамках обычной двоичной логики сначала рассмотреть предикат о существовании решения (либо существует, либо нет), а затем о движении (если существует, то либо движется, либо покоится). А в случае деформируемой системы, наоборот, сначала рассмотреть предикат движения, а потом устойчивости. Но на мой взгляд, в силу нескольких достаточно тонких причин, такой подход не слишком изящен. Во-первых, в механике обычно предполагается, что данные начальные условия всегда определяют решение. Преположение, что решения может не быть и введение предиката «Существует решение(Система)=false» — скандал! В троичной же логике скандала нет, «не определено» мыслится как равное состояние покою и движению. Во-вторых, как уже говорилось, есть системы, для которых в пределе абсолютной жесткости неустйчивость соответcтвует парадоксу. В троичной логике очень легко сказать, что «неустойчивость» в пределе соответствует «нет решения». В обычной бинарной же логике это не так, да и очередность пpименения предикатов приходитcя менять.

Этой странной теме посвящена моя статья в журнале, и я надеюсь довести ее до более интересных результатов.
M Nosonovsky, 2018, Logical and information aspects in surface science: friction, capillarity, and superhydrophobicity Int. J. Parallel, Emergent and Distributed Sys. (in press) http://dx.doi.org/10.1080/17445760.2017.1419350

Мою заметку о методологических проблемах современной механики можно прочитать здесь:
Методологичекие проблемы механики: между метафизикой и махизмом http://blogs.7iskusstv.com/?p=58491
а заметку о философских аспектах трения — здесь:
М. Носоновский Про трение как “сопутствующее явление” // «Семь искусств», Номер 9(78) сентябрь 2016 года http://7iskusstv.com/2016/Nomer9/Nosonovsky1.php